🚨 'C언어로 쉽게 풀어쓴 자료구조' 라는 책을 활용했던 과거 수업 필기를 정리한 것입니다.
💡 Chapter 순서는 책과 같지만 교수님의 과거 수업 내용에 따라 일부 책과 다른 내용이 있습니다.
※ n개의 데이터 sorting 하는데 걸리는 최소의 시간 nlg n
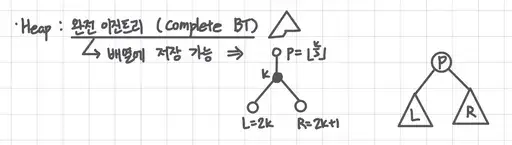
Heap 의 성질
- P >= L, R (Max Heap)
- P <= L, R ( Min Heap)
- 삭제할 때 root를 삭제
1. 삽입 (Insert)
- 맨 끝에 추가 (Size 증가)
- 추가된 원소를 Heap이 되도록 올려보냄 (재귀적)


2. 삭제 (Delete)
- root (최대값)를 삭제 (service)
- 맨 끝 원소를 root로 이동 (size 감소)
- root를 Heap이 되도록 내려보냄 (재귀적)


3. 초기 Heap 구성 (Heap Building)
배열 H[1, ... N]에 N개의 Data
- Top - Down (하향식 구성)

- Bottom - Up (상향식 구성)

4. Why Bottom - Up faster than Top - Down?
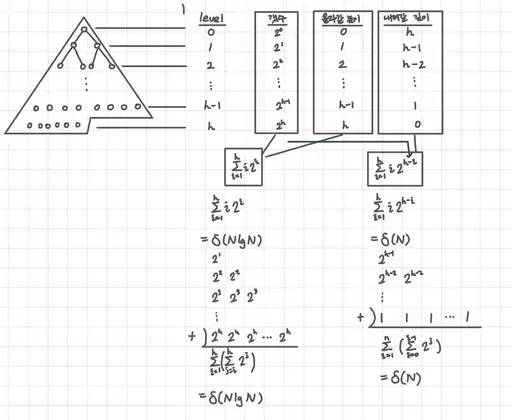
5. Heap Sorting
heap을 구성한 후 root를 N번 (정확히는 N-1번) 삭제하여 나열함으로 sorting -> O(Nlg N)
A[1, ..., N]
1. Building-Heap // Bottom - Up -> O(N)
2. for(k = N down to 2) {
swap(A[1], A[k]) // 삭제
HeapDown(1, k-1) // 재정비
}
6. Heap Python 구현
# heap
# 그림 , 구현 할 줄 알아야함
# heap 자료 구조 : 완벽한 이진트리의 형태로 자료를 저장하고 빼냄 => O(nlogn)
# 1차 배열로 트리에 저장하기
arr = [4,7,8,1,5,3,6,9] # Maxheap
heep = [0] * 20
hindex = 1 # 힙 이라는 1차배열의 인덱스 역할
def insert(value):
global heap,hindex
heap[hindex] = value
now = hindex
hindex += 1
while 1:
parents = now//2 # 부모 인덱스 확인
if parents == 0 : break # 처음에 인덱스가 1이면 그냥 끄기
if heap[parents] > heap[now] : break # 부모가 더 크면 break
heap[parents],heap[now] = heap[now],heap[parents] # 부모가 지금 들어온 애보다 작으면 스왑왑
now = parents #부모를 그 다음 now로 놓고 위로 오라가면서 그 다음 부모랑 비교.
def top():
global heap
return heap[1] # 루트노드(1번 인덱스의 값) 리턴
def pop():
global heap,hindex
heap[1] = heap[hindex-1] # 맨 뒤의 값을 루트로 일단 옮기기
heap[hindex] = 0
hindex -= 1
now = 1
while 1:
son = now * 2 # 왼쪽 자식
rson = son+1 # 오른쪽 자식
# 오른쪽에 자식이 있고 왼쪽 자식보다 오른쪽 자식 값이 더 크면 자식을 오른쪽 자식으로 선택
if heap[rson] != 0 and heap[son] < heap[rson] : son = rson
if heap[now] >= heap[son] : break # 부모가 내가 찜한 자식보다 크면 브레이크
heap[now],heap[son] = heap[son],heap[now] # 그게 아니면 스왑
now = son # 트리의 밑으로 내려가면서 while 돌며 그 밑의 자식과 비교교
for i in range(len(arr)):
insert(arr[i]) # 트리의 형태로 저장(1차배열)
for i in range(len(arr)):
print(top(),end=' ') # 루트노드 출력
pop() # 맨 뒤에 있는 아이를 1번 인덱스로 올리고 자식들이랑 비교'이론공부 > 자료구조' 카테고리의 다른 글
| Chapter 07. 트리(Tree) (0) | 2022.04.04 |
|---|---|
| Chapter 06. 큐(Queue) (0) | 2021.06.15 |
| Chapter 05. 스택(Stack) (0) | 2021.06.11 |
| Chapter 04. List (0) | 2021.06.10 |
| Chapter 03. 배열, 구조체, 포인터 (0) | 2021.06.10 |




댓글